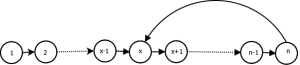
Fix loop in a linked list
Cycle or loop in a linked list with ![]() nodes is shown in pictorial representation.
nodes is shown in pictorial representation.
In this picture the number of nodes in the list is ![]() and the last node points to node at a position x(which created the cycle). From the picture it is obvious that to fix the loop:
and the last node points to node at a position x(which created the cycle). From the picture it is obvious that to fix the loop:
- Find the last element
- Correct it to point end(NULL)
In the above steps, step 1(find the last element) is little difficult if total number of nodes in the list is unknown. In this post I will describe a method I discovered to find the last node. I drew couple of pictures to explain the complexity of the problem. The following pictures explains the same loop condition but in different form. It explains why it is hard to find the last node.

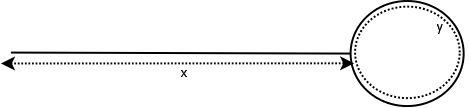
The illustration also tells us the following
![]()
where
![]() is total number of nodes in the list
is total number of nodes in the list
![]() is number of nodes before the cycle starts.
is number of nodes before the cycle starts.
![]() is number of nodes forming the cycle.
is number of nodes forming the cycle.
If we have value of ![]() and
and ![]() then the equation can be solved, which will give the last node’s location.
then the equation can be solved, which will give the last node’s location.
Finding ![]()
- Detect the cycle using Floyd’s Cycle detection algorithm. (Two pointer with varying speed)
- When cycle is detected
- Store the current node as H
- Move to next node and increment y(y++)
- If current node is H then exit
- Goto step 2
Finding ![]()
Let’s first see the easiest way to solve this:
- Have two pointers (p1, p2)
- p1 = node 0
- p2 = p1 + y nodes
- if p1 == p2 then we found the result is
- p1 = p1 + y nodes
- goto step 3.
The complexity of this algorithm linear depends on ![]() . For example if
. For example if ![]() is 10K and
is 10K and ![]() is 2 then number of node visits are > 20K. In other words the complexity is
is 2 then number of node visits are > 20K. In other words the complexity is ![]() .
.
I believe it can be done in ![]() or
or ![]() with following method This following diagram captures state when the “tortoise and the hare” algorithm detects the cycle.
with following method This following diagram captures state when the “tortoise and the hare” algorithm detects the cycle.
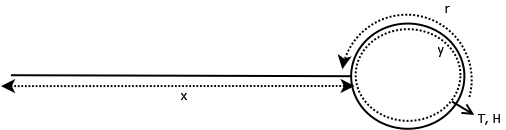
Lets define few more variables at the time of cycle detection:
![]() is the total number of nodes tortoise traveled.
is the total number of nodes tortoise traveled.
![]() is the total number of nodes hare traveled.
is the total number of nodes hare traveled.
![]() can be defined as number of nodes before the ‘last node’
can be defined as number of nodes before the ‘last node’
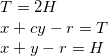
where c is the number of complete cycles hare covered.
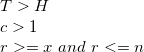
From this we can derive
![]()
Using value of ![]() ,
, ![]() can be derived.
can be derived.
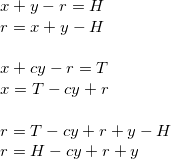
Using this formula ![]() can be found. With this
can be found. With this ![]() value, the last node can be found by travelling
value, the last node can be found by travelling ![]() nodes where T and H met.
nodes where T and H met.